Power of Compounding - Secret to Wealth Creation

The easiest and the simplest form of calculating interest on your investments is simple interest. Simple interest is the interest earned on the initial investment made. Say, you have invested ₹ 1,00,000 at 12% per annum for a period of fifteen years with returns calculated by using simple interest.



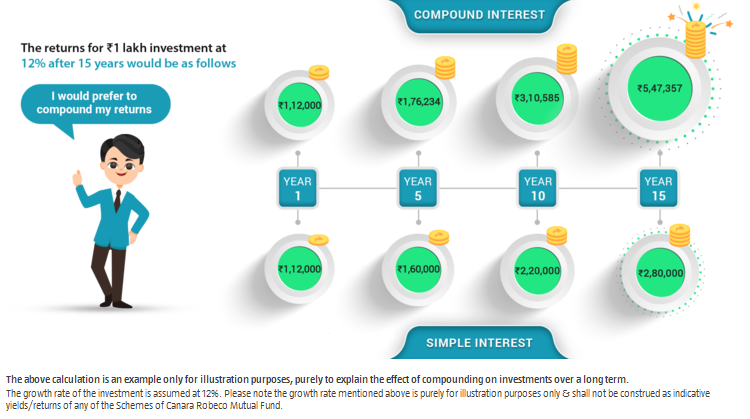
The interest earned at the end of three years would be ₹ 2,80,000 i.e. ₹ 12,000 each year. Here, the base for calculating interest remains constant. Generally, term deposits which are for less than six months offer simple interest. Most financial products, however, work on the principle of compounded interest. Compounding of interest is nothing but computing interest on the initial amount invested and also on the accumulated interest of previous periods. Simply put, it is earning interest on interest.

Continuing with our earlier illustration, if ₹ 1,00,000 is invested at 12% p.a. compounded annually, at the end of three years, the interest earned would be ₹ 4,47,356.58 . Unlike simple interest, the base for interest calculation increases every year as the interest is re-invested. In the above illustration, the difference between the two is low since the amount invested is for a lesser duration and the frequency of compounding is only annual.

The difference becomes more significant with longer periods and more frequent compounding as simple interest grows in a linear fashion while compound interest grows exponentially. While compound interest is better than simple interest, there are three points you should keep in mind to harness the power of compounding:

Start early

The longer the investment horizon, the more the interest on interest earned and hence you have time working to your advantage.

 

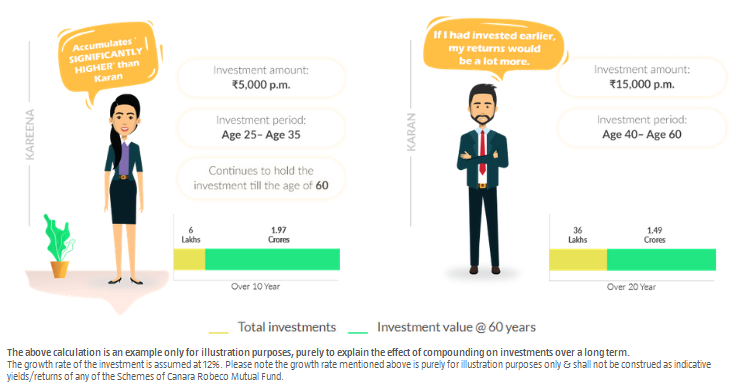
Let's take an example. Both Karan and Kareena are 60 years old and are friends who reunited after a very long time. Both of them are discussing about the investments they had made when they were young. Both of them invested different sums of money for a period of 10 years i.e. Karan invested ₹ 15,000 every month whereas Kareena invested only ₹ 5,000 every month. Karan started the investments when he was 35 years old till he turned 45 while Kareena started investing from her 25th Birthday till she turned 35. Both of them continued to hold their investments till they turned 60. On her 60th Birthday the value of the ₹ 6 Lacs invested by Kareena had reached ₹ 1.97 Crores, but Karan's investments of ₹ 36 Lacs had only become ₹ 1.49 Crores, even though Karan invested more money than Kareena. How is this possible?

Karan's started his investments when he was 35 and Kareena when she was 25. At 60, Kareena's money was invested in the avenue since she was 25 i.e. for 35 years while Karan's funds remained invested only for 25 Years. Kareena's money got compounded for 10 extra years and hence made a lot of difference today. Hence, it is said, starting early is always beneficial for accumulating significantly higher returns than starting to invest at a later stage.

Shorter interval, greater impact

Compounding cycle is nothing but the frequency or interval at which the interest multiplies. Compounding can be done on daily, monthly, quarterly, half yearly or annual basis.

The shorter the interval of compounding, the greater the impact. This can be understood with the help of the following illustration.

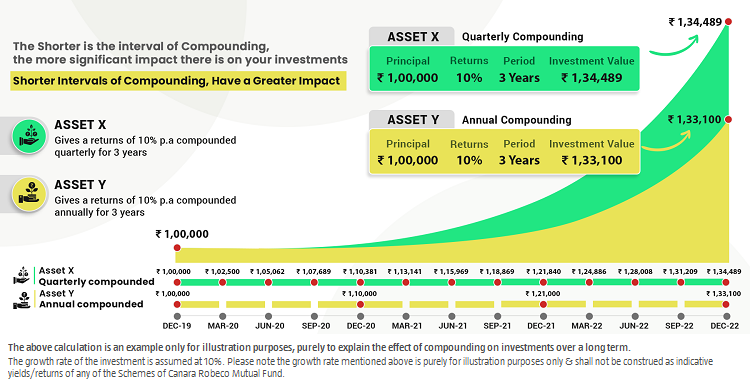
Ram invests ₹ 1,00,000 in two asset classes for a period of three years. Asset X gives a return of 10% p.a. compounded quarterly, while asset Y gives same return of 10% p.a. but is compounded annually. At the end of three years, the value of Asset X is ₹ 1,34,489 while that of Asset Y is ₹ 1,33,100. As the frequency of compounding increases, the difference becomes significant.

Higher the rate, more you gain Higher the rate of returns, the more you can accumulate. No wonder why experts advise investing in equities if one has a long investment horizon; they offer a better potential rate of return over the long term. This is the magic of compounding and you only need to keep these small points in mind to make this magic happen for you. As the famous Einstein quote goes "He, who understands the power of compounding, earns it and he who doesn't pays it".